Preprocessing and clustering 3k PBMCs

Translator: Alex Wolf

In May 2017, this started out as a demonstration that Scanpy would allow to reproduce most of Seurat’s (Satija et al., 2015) guided clustering tutorial. We gratefully acknowledge the authors of Seurat for the tutorial. In the meanwhile, we have added and removed a few pieces.

The data consists in 3k PBMCs from a Healthy Donor and is freely available from 10x Genomics (here from this webpage). On a unix system, you can uncomment and run the following to download and unpack the data

# !mkdir data
# !wget http://cf.10xgenomics.com/samples/cell-exp/1.1.0/pbmc3k/pbmc3k_filtered_gene_bc_matrices.tar.gz -O data/pbmc3k_filtered_gene_bc_matrices.tar.gz
# !cd data; tar -xzf pbmc3k_filtered_gene_bc_matrices.tar.gz

Note

Download the notebook by clicking on the Edit on GitHub button. On GitHub, you can download using the Raw button via right-click and Save Link As. Alternatively, download the whole scanpy-tutorial repository.

Note

In Jupyter notebooks and lab, you can see the documentation for a python function by hitting SHIFT + TAB. Hit it twice to expand the view.

import numpy as np
import pandas as pd
import scanpy as sc

sc.settings.verbosity = 3             # verbosity: errors (0), warnings (1), info (2), hints (3)
sc.logging.print_versions()
sc.settings.set_figure_params(dpi=80)

scanpy==1.4.5 anndata==0.6.22.post1 umap==0.3.8 numpy==1.16.3 scipy==1.3.0 pandas==0.23.4 scikit-learn==0.22 statsmodels==0.10.0 python-igraph==0.7.1 louvain==0.6.1

results_file = './write/pbmc3k.h5ad'  # the file that will store the analysis results

adata = sc.read_10x_mtx(
    './data/filtered_gene_bc_matrices/hg19/',  # the directory with the `.mtx` file
    var_names='gene_symbols',                  # use gene symbols for the variable names (variables-axis index)
    cache=True)                                # write a cache file for faster subsequent reading

... reading from cache file cache/data-filtered_gene_bc_matrices-hg19-matrix.h5ad

adata.var_names_make_unique()  # this is unnecessary if using `var_names='gene_ids'` in `sc.read_10x_mtx`

adata

AnnData object with n_obs × n_vars = 2700 × 32738
    var: 'gene_ids'

Preprocessing

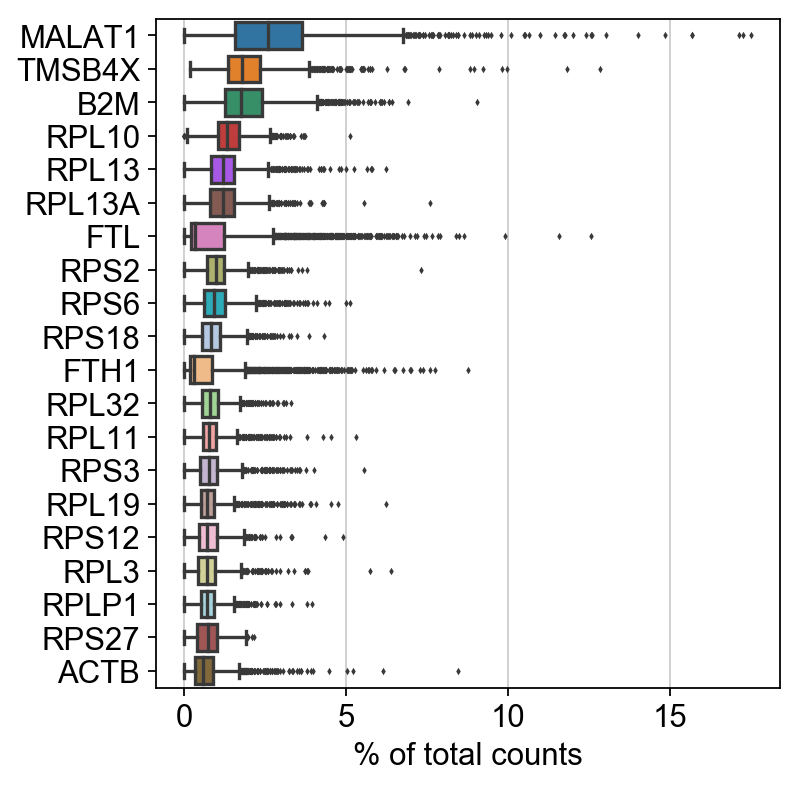
Show those genes that yield the highest fraction of counts in each single cells, across all cells.

sc.pl.highest_expr_genes(adata, n_top=20, )

normalizing counts per cell
    finished (0:00:00)

Basic filtering.

sc.pp.filter_cells(adata, min_genes=200)
sc.pp.filter_genes(adata, min_cells=3)

filtered out 19024 genes that are detected in less than 3 cells

Let us assemple some information about mitochondrial genes, which are important for quality control.

Citing from “Simple Single Cell” workflows (Lun, McCarthy & Marioni, 2017):

High proportions are indicative of poor-quality cells (Islam et al. 2014; Ilicic et al. 2016), possibly because of loss of cytoplasmic RNA from perforated cells. The reasoning is that mitochondria are larger than individual transcript molecules and less likely to escape through tears in the cell membrane.

Note you can also use the function pp.calculate_qc_metrics to compute the fraction of mitochondrial genes and additional measures.

mito_genes = adata.var_names.str.startswith('MT-')
# for each cell compute fraction of counts in mito genes vs. all genes
# the `.A1` is only necessary as X is sparse (to transform to a dense array after summing)
adata.obs['percent_mito'] = np.sum(
    adata[:, mito_genes].X, axis=1).A1 / np.sum(adata.X, axis=1).A1
# add the total counts per cell as observations-annotation to adata
adata.obs['n_counts'] = adata.X.sum(axis=1).A1

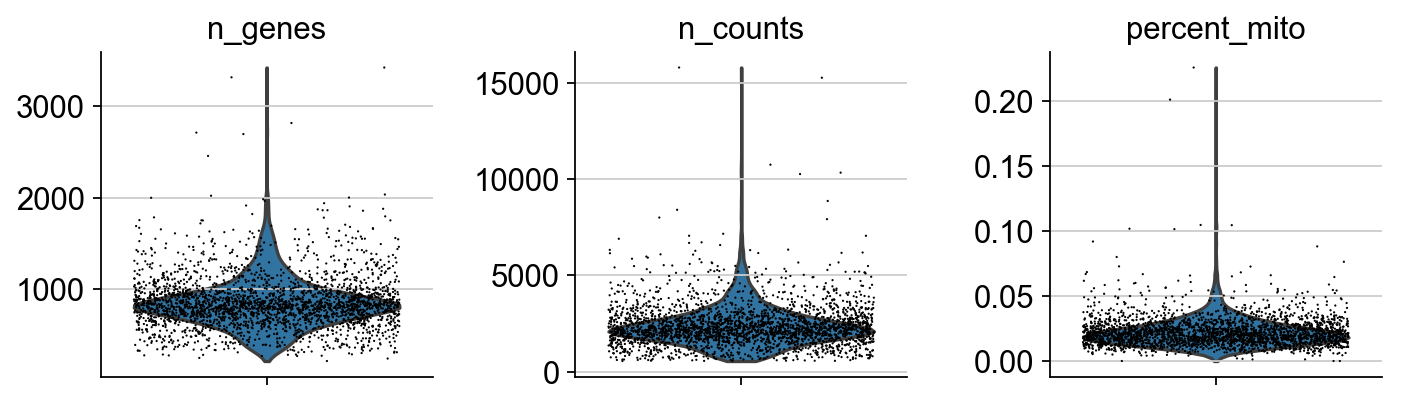
A violin plot of the computed quality measures.

sc.pl.violin(adata, ['n_genes', 'n_counts', 'percent_mito'],
             jitter=0.4, multi_panel=True)

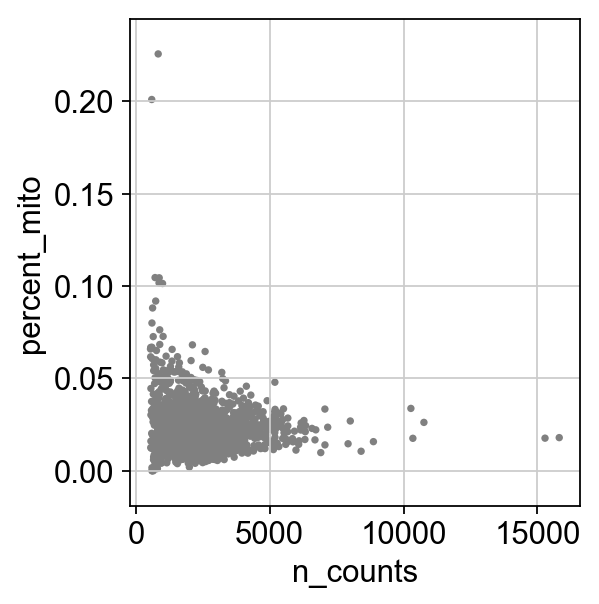
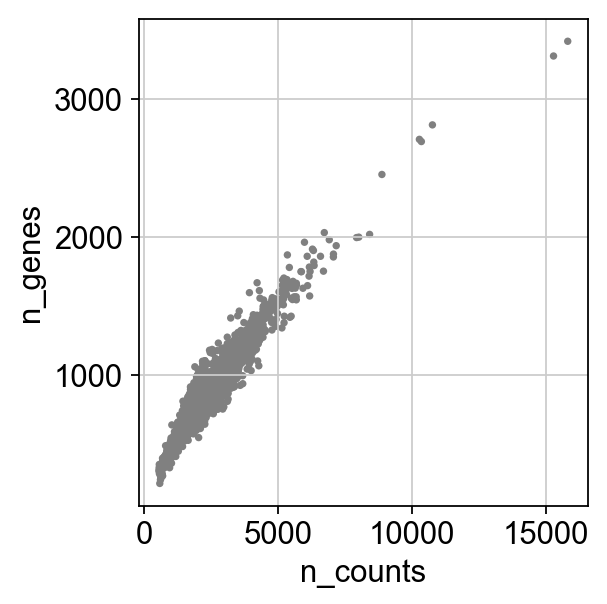
Remove cells that have too many mitochondrial genes expressed or too many total counts.

sc.pl.scatter(adata, x='n_counts', y='percent_mito')
sc.pl.scatter(adata, x='n_counts', y='n_genes')

adata

AnnData object with n_obs × n_vars = 2700 × 13714
    obs: 'n_genes', 'percent_mito', 'n_counts'
    var: 'gene_ids', 'n_cells'

Actually do the filtering.

adata = adata[adata.obs.n_genes < 2500, :]
adata = adata[adata.obs.percent_mito < 0.05, :]

Total-count normalize (library-size correct) the data matrix \(\mathbf{X}\) to 10,000 reads per cell, so that counts become comparable among cells.

sc.pp.normalize_total(adata, target_sum=1e4)

normalizing counts per cell
    finished (0:00:01)

Logarithmize the data.

sc.pp.log1p(adata)

Set the .raw attribute of AnnData object to the normalized and logarithmized raw gene expression for later use in differential testing and visualizations of gene expression. This simply freezes the state of the AnnData object.

While many people consider the normalized data matrix as the “relevant data” for visualization and differential testing, some would prefer to store the unnormalized data in .raw.

adata.raw = adata

Note

If you don’t proceed below with correcting the data with sc.pp.regress_out and scaling it via sc.pp.scale, you can also get away without using .raw at all.

The result of the following highly-variable-genes detection is stored as an annotation in .var.highly_variable and auto-detected by PCA and hence, sc.pp.neighbors and subsequent manifold/graph tools. In that case, the step actually do the filtering below is unnecessary, too.

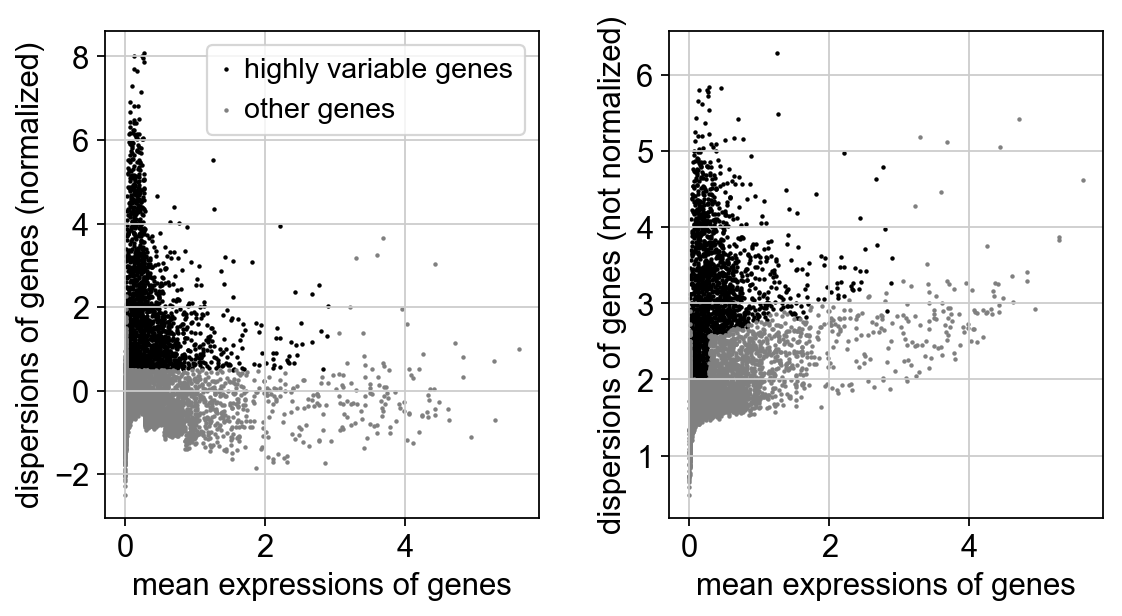
Identify highly-variable genes.

sc.pp.highly_variable_genes(adata, min_mean=0.0125, max_mean=3, min_disp=0.5)

extracting highly variable genes
    finished (0:00:00)
--> added
    'highly_variable', boolean vector (adata.var)
    'means', float vector (adata.var)
    'dispersions', float vector (adata.var)
    'dispersions_norm', float vector (adata.var)

sc.pl.highly_variable_genes(adata)

Actually do the filtering.

adata = adata[:, adata.var.highly_variable]

Regress out effects of total counts per cell and the percentage of mitochondrial genes expressed. Scale the data to unit variance.

sc.pp.regress_out(adata, ['n_counts', 'percent_mito'])

regressing out ['n_counts', 'percent_mito']
    sparse input is densified and may lead to high memory use
    finished (0:00:04)

Scale each gene to unit variance. Clip values exceeding standard deviation 10.

sc.pp.scale(adata, max_value=10)

Principal component analysis

Reduce the dimensionality of the data by running principal component analysis (PCA), which reveals the main axes of variation and denoises the data.

sc.tl.pca(adata, svd_solver='arpack')

computing PCA with n_comps = 50
    on highly variable genes
    finished (0:00:00)

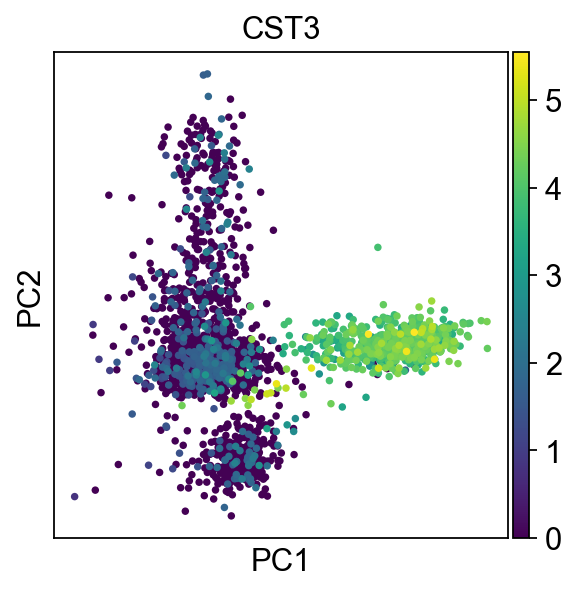
We can make a scatter plot in the PCA coordinates, but we will not use that later on.

sc.pl.pca(adata, color='CST3')

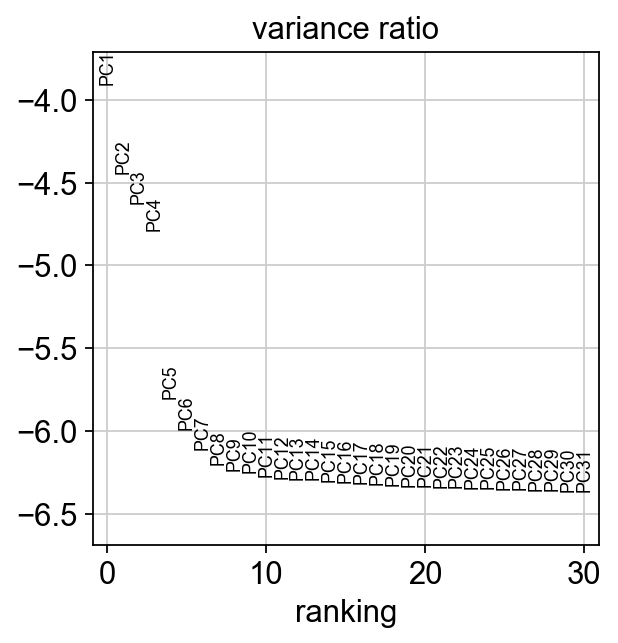
Let us inspect the contribution of single PCs to the total variance in the data. This gives us information about how many PCs we should consider in order to compute the neighborhood relations of cells, e.g. used in the clustering function sc.tl.louvain() or tSNE sc.tl.tsne(). In our experience, often, a rough estimate of the number of PCs does fine.

sc.pl.pca_variance_ratio(adata, log=True)

Save the result.

adata.write(results_file)

adata

AnnData object with n_obs × n_vars = 2638 × 1838
    obs: 'n_genes', 'percent_mito', 'n_counts'
    var: 'gene_ids', 'n_cells', 'highly_variable', 'means', 'dispersions', 'dispersions_norm'
    uns: 'log1p', 'pca'
    obsm: 'X_pca'
    varm: 'PCs'

Computing the neighborhood graph

Let us compute the neighborhood graph of cells using the PCA representation of the data matrix. You might simply use default values here. For the sake of reproducing Seurat’s results, let’s take the following values.

sc.pp.neighbors(adata, n_neighbors=10, n_pcs=40)

computing neighbors
    using 'X_pca' with n_pcs = 40
    finished: added to `.uns['neighbors']`
    'distances', distances for each pair of neighbors
    'connectivities', weighted adjacency matrix (0:00:03)

Embedding the neighborhood graph

We advertise embedding the graph in 2 dimensions using UMAP (McInnes et al., 2018), see below. It is potentially more faithful to the global connectivity of the manifold than tSNE, i.e., it better preservers trajectories. In some ocassions, you might still observe disconnected clusters and similar connectivity violations. They can usually be remedied by running:

tl.paga(adata)
pl.paga(adata, plot=False)  # remove `plot=False` if you want to see the coarse-grained graph
tl.umap(adata, init_pos='paga')

sc.tl.umap(adata)

computing UMAP
    finished: added
    'X_umap', UMAP coordinates (adata.obsm) (0:00:04)

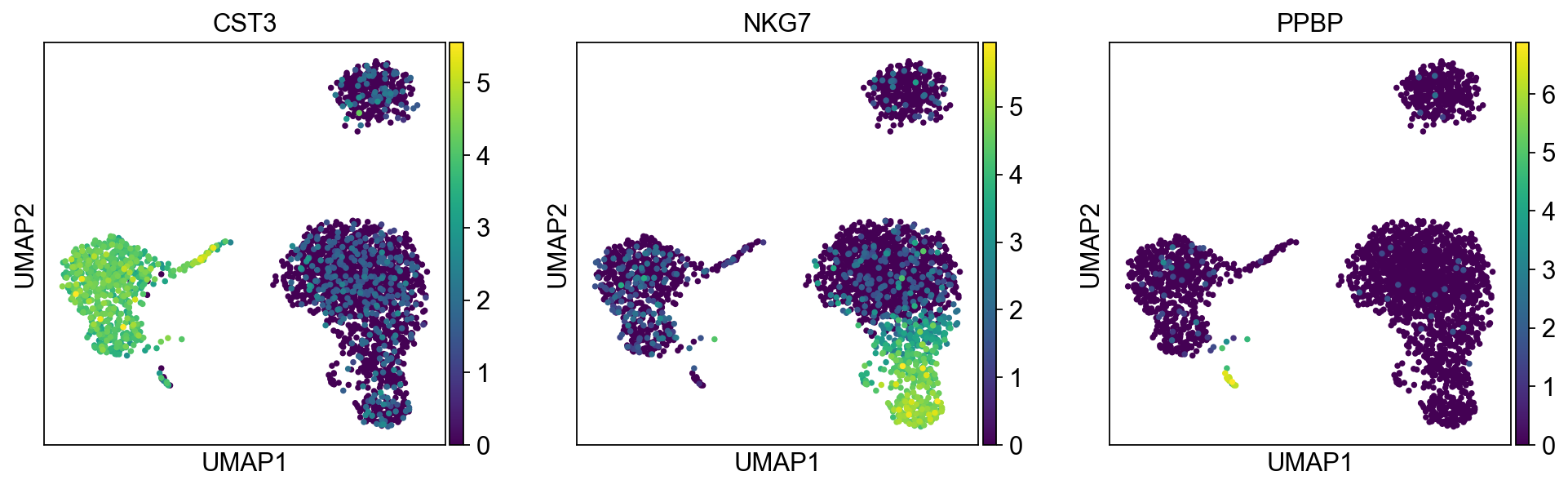
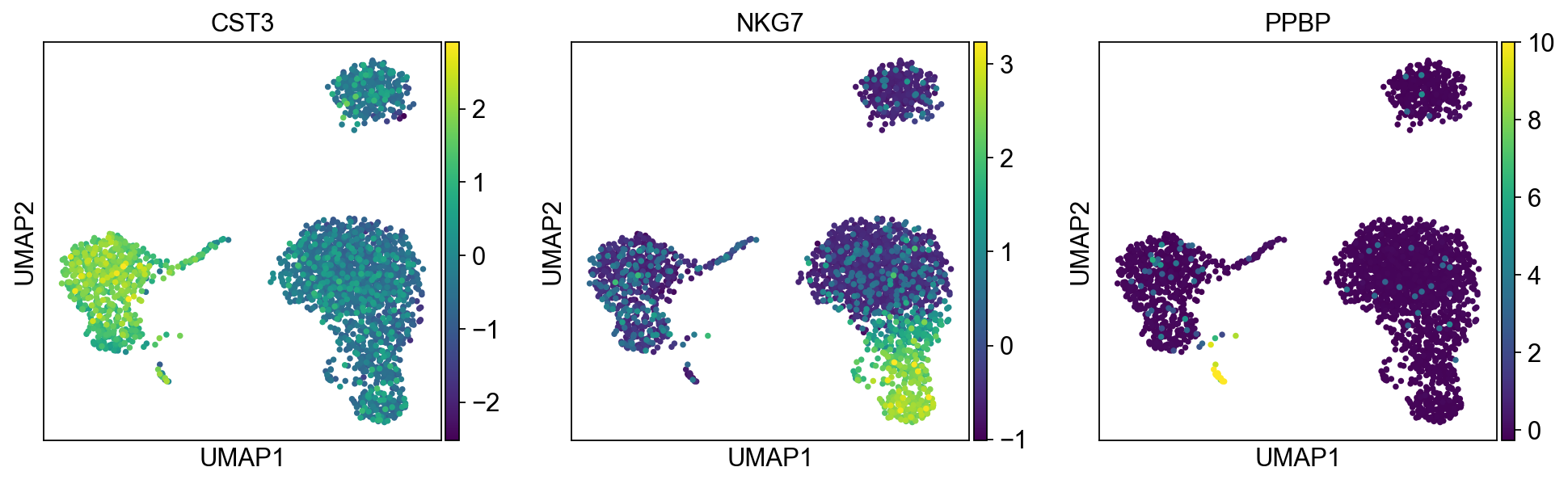
sc.pl.umap(adata, color=['CST3', 'NKG7', 'PPBP'])

As we set the .raw attribute of adata, the previous plots showed the “raw” (normalized, logarithmized, but uncorrected) gene expression. You can also plot the scaled and corrected gene expression by explicitly stating that you don’t want to use .raw.

sc.pl.umap(adata, color=['CST3', 'NKG7', 'PPBP'], use_raw=False)

Clustering the neighborhood graph

As Seurat and many others, we recommend the Leiden graph-clustering method (community detection based on optimizing modularity) by Traag *et al.* (2018). Note that Leiden clustering directly clusters the neighborhood graph of cells, which we already computed in the previous section.

sc.tl.leiden(adata)

running Leiden clustering
    finished: found 8 clusters and added
    'leiden', the cluster labels (adata.obs, categorical) (0:00:00)

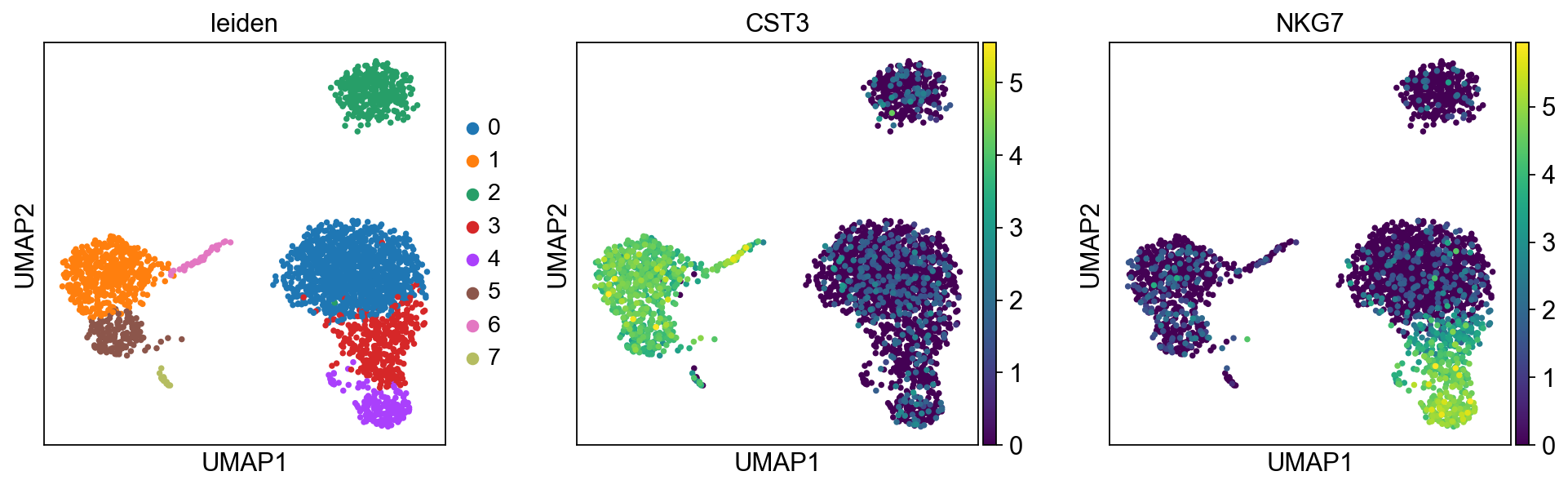
Plot the clusters, which agree quite well with the result of Seurat.

sc.pl.umap(adata, color=['leiden', 'CST3', 'NKG7'])

Save the result.

adata.write(results_file)

Finding marker genes

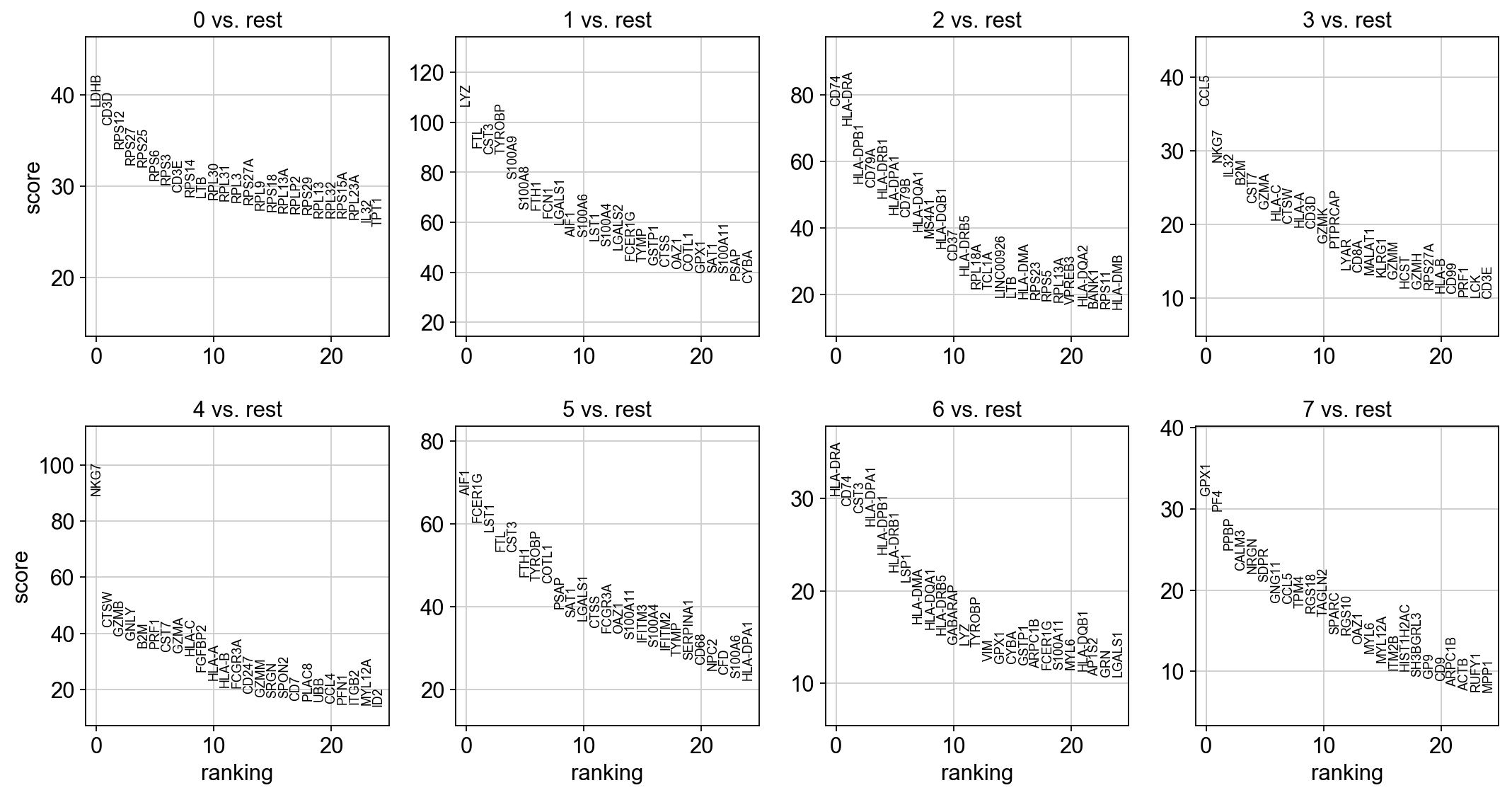
Let us compute a ranking for the highly differential genes in each cluster. For this, by default, the .raw attribute of AnnData is used in case it has been initialized before. The simplest and fastest method to do so is the t-test.

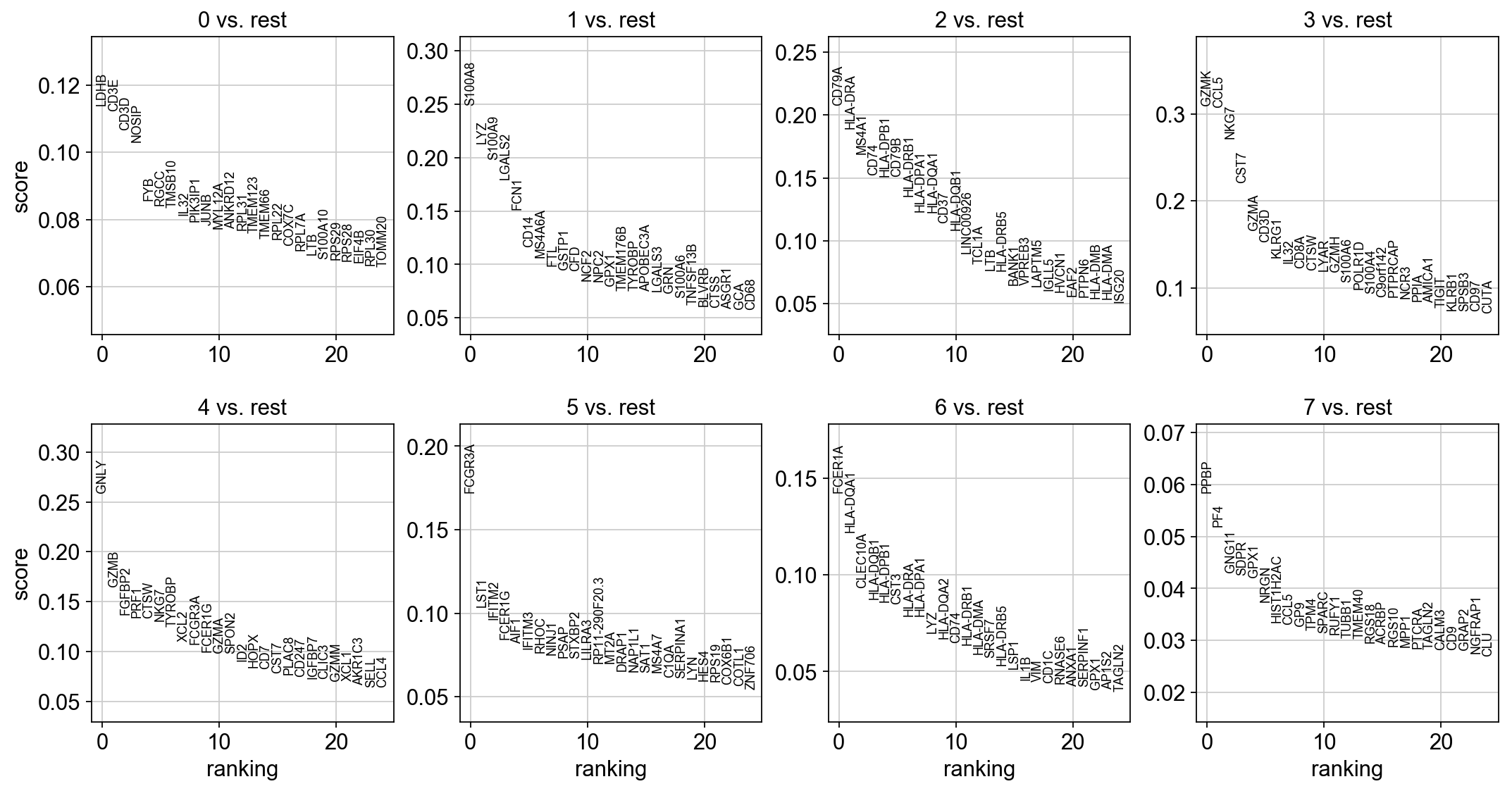
sc.tl.rank_genes_groups(adata, 'leiden', method='t-test')
sc.pl.rank_genes_groups(adata, n_genes=25, sharey=False)

ranking genes
    finished: added to `.uns['rank_genes_groups']`
    'names', sorted np.recarray to be indexed by group ids
    'scores', sorted np.recarray to be indexed by group ids
    'logfoldchanges', sorted np.recarray to be indexed by group ids
    'pvals', sorted np.recarray to be indexed by group ids
    'pvals_adj', sorted np.recarray to be indexed by group ids (0:00:00)

sc.settings.verbosity = 2  # reduce the verbosity

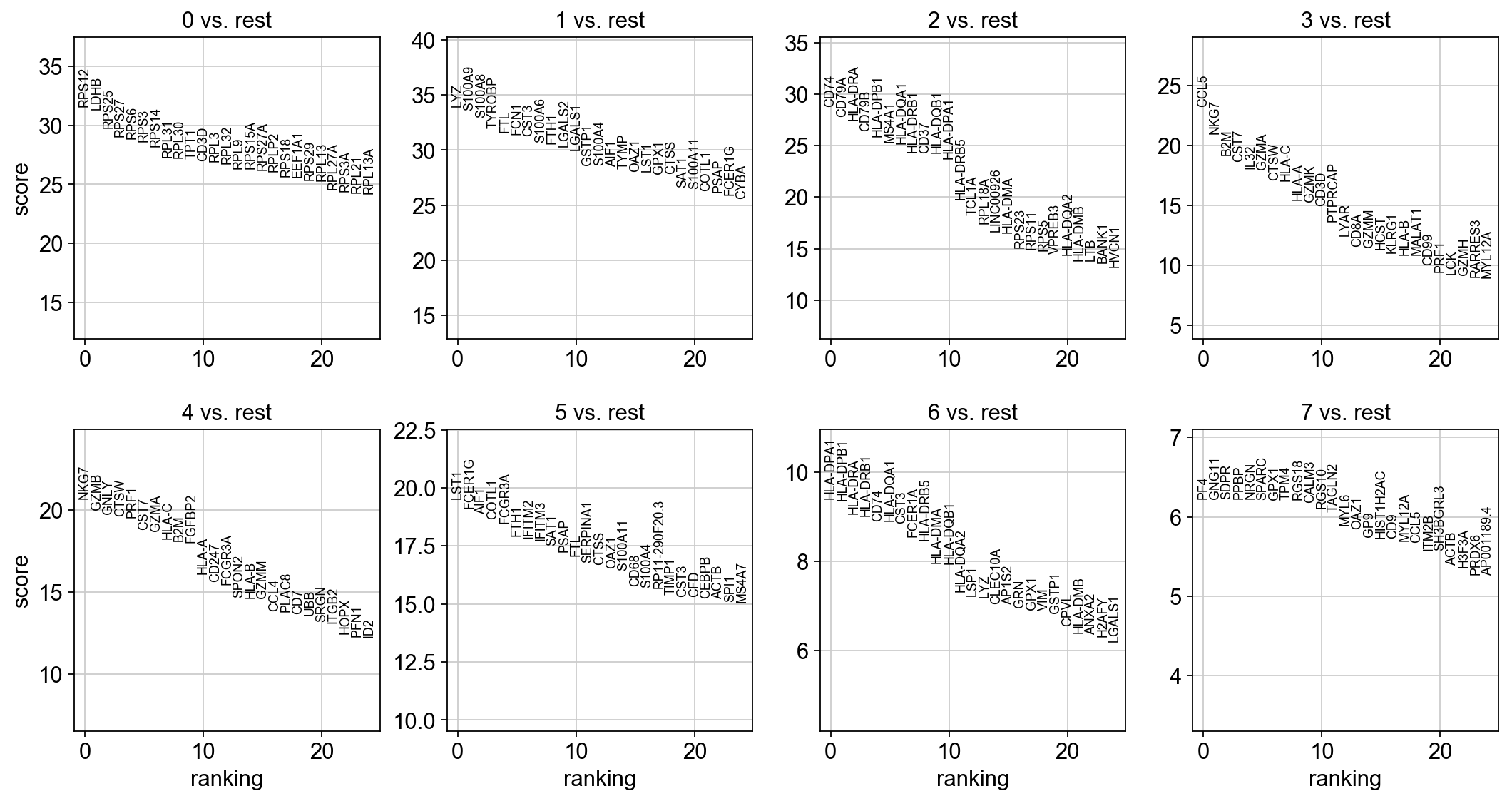
The result of a Wilcoxon rank-sum (Mann-Whitney-U) test is very similar. We recommend using the latter in publications, see e.g., Sonison & Robinson (2018). You might also consider much more powerful differential testing packages like MAST, limma, DESeq2 and, for python, the recent diffxpy.

sc.tl.rank_genes_groups(adata, 'leiden', method='wilcoxon')
sc.pl.rank_genes_groups(adata, n_genes=25, sharey=False)

ranking genes
    finished (0:00:02)

Save the result.

adata.write(results_file)

As an alternative, let us rank genes using logistic regression. For instance, this has been suggested by Natranos et al. (2018). The essential difference is that here, we use a multi-variate appraoch whereas conventional differential tests are uni-variate. Clark et al. (2014) has more details.

sc.tl.rank_genes_groups(adata, 'leiden', method='logreg')
sc.pl.rank_genes_groups(adata, n_genes=25, sharey=False)

ranking genes
    finished (0:00:05)

With the exceptions of IL7R, which is only found by the t-test and FCER1A, which is only found by the other two appraoches, all marker genes are recovered in all approaches.

Louvain Group	Markers	Cell Type
0	IL7R	CD4 T cells
1	CD14, LYZ	CD14+ Monocytes
2	MS4A1	B cells
3	CD8A	CD8 T cells
4	GNLY, NKG7	NK cells
5	FCGR3A, MS4A7	FCGR3A+ Monocytes
6	FCER1A, CST3	Dendritic Cells
7	PPBP	Megakaryocytes

Let us also define a list of marker genes for later reference.

marker_genes = ['IL7R', 'CD79A', 'MS4A1', 'CD8A', 'CD8B', 'LYZ', 'CD14',
                'LGALS3', 'S100A8', 'GNLY', 'NKG7', 'KLRB1',
                'FCGR3A', 'MS4A7', 'FCER1A', 'CST3', 'PPBP']

Reload the object that has been save with the Wilcoxon Rank-Sum test result.

adata = sc.read(results_file)

Show the 10 top ranked genes per cluster 0, 1, …, 7 in a dataframe.

pd.DataFrame(adata.uns['rank_genes_groups']['names']).head(5)

	0	1	2	3	4	5	6	7
0	RPS12	LYZ	CD74	CCL5	NKG7	LST1	HLA-DPA1	PF4
1	LDHB	S100A9	CD79A	NKG7	GZMB	FCER1G	HLA-DPB1	GNG11
2	RPS25	S100A8	HLA-DRA	B2M	GNLY	AIF1	HLA-DRA	SDPR
3	RPS27	TYROBP	CD79B	CST7	CTSW	COTL1	HLA-DRB1	PPBP
4	RPS6	FTL	HLA-DPB1	IL32	PRF1	FCGR3A	CD74	NRGN

Get a table with the scores and groups.

result = adata.uns['rank_genes_groups']
groups = result['names'].dtype.names
pd.DataFrame(
    {group + '_' + key[:1]: result[key][group]
    for group in groups for key in ['names', 'pvals']}).head(5)

	0_n	0_p	1_n	1_p	2_n	2_p	3_n	3_p	4_n	4_p	5_n	5_p	6_n	6_p	7_n	7_p
0	RPS12	4.806932e-219	LYZ	1.007060e-252	CD74	3.043536e-182	CCL5	1.340647e-119	NKG7	4.689070e-95	LST1	5.650219e-85	HLA-DPA1	5.422417e-21	PF4	4.722886e-10
1	LDHB	5.645430e-216	S100A9	3.664292e-248	CD79A	6.860832e-170	NKG7	5.020256e-98	GZMB	2.381363e-89	FCER1G	1.697236e-81	HLA-DPB1	7.591860e-21	GNG11	4.733899e-10
2	RPS25	3.355677e-195	S100A8	9.457377e-239	HLA-DRA	8.398068e-166	B2M	3.800068e-82	GNLY	9.322195e-87	AIF1	1.377723e-79	HLA-DRA	1.306768e-19	SDPR	4.733899e-10
3	RPS27	3.322679e-185	TYROBP	2.209430e-224	CD79B	1.171444e-153	CST7	5.664351e-78	CTSW	1.035081e-85	COTL1	9.684016e-78	HLA-DRB1	1.865104e-19	PPBP	4.744938e-10
4	RPS6	2.400370e-183	FTL	3.910903e-219	HLA-DPB1	6.167786e-148	IL32	6.704290e-73	PRF1	3.364126e-85	FCGR3A	2.516161e-76	CD74	5.853161e-19	NRGN	4.800511e-10

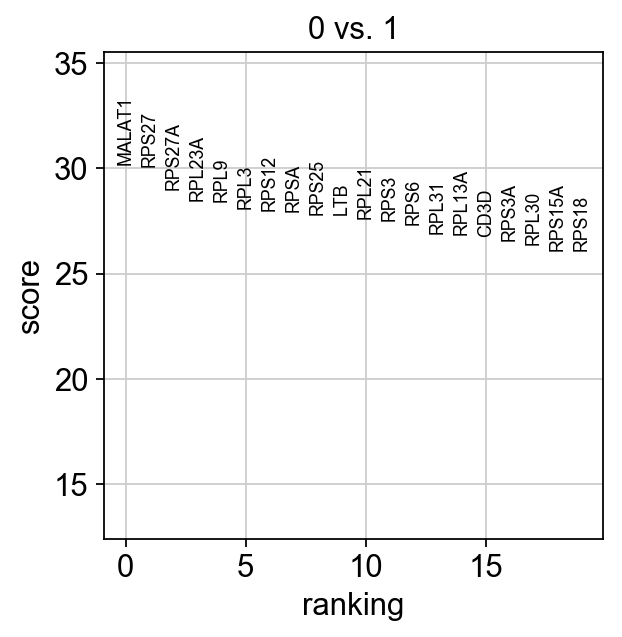
Compare to a single cluster.

sc.tl.rank_genes_groups(adata, 'leiden', groups=['0'], reference='1', method='wilcoxon')
sc.pl.rank_genes_groups(adata, groups=['0'], n_genes=20)

ranking genes
    finished (0:00:01)

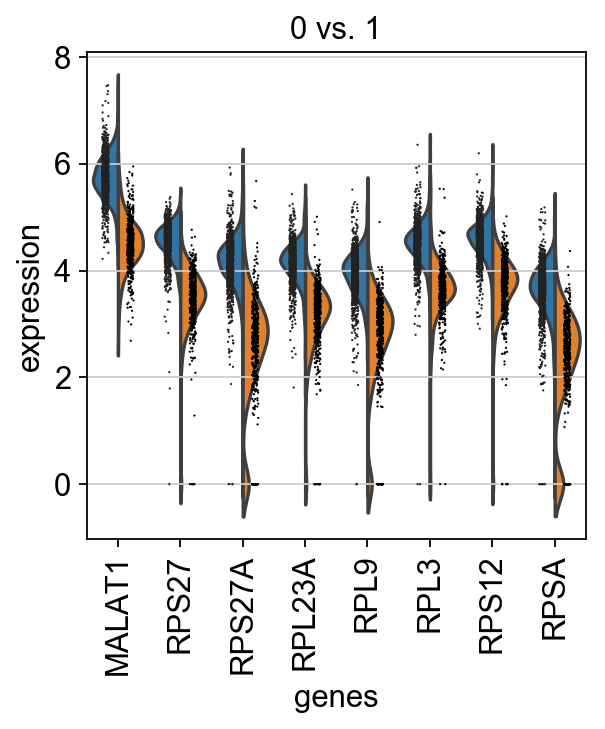
If we want a more detailed view for a certain group, use sc.pl.rank_genes_groups_violin.

sc.pl.rank_genes_groups_violin(adata, groups='0', n_genes=8)

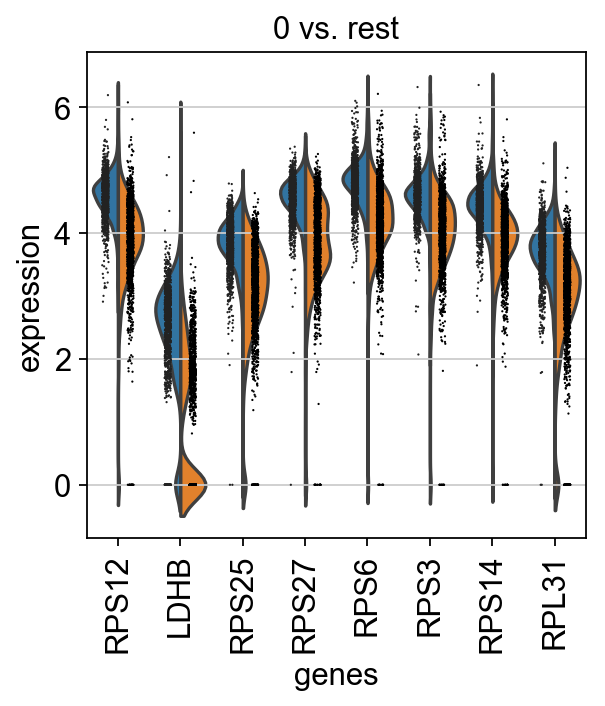
Reload the object that computed differential expression by comparing to the rest of the groups.

adata = sc.read(results_file)

sc.pl.rank_genes_groups_violin(adata, groups='0', n_genes=8)

If you want to compare a certain gene across groups, use the following.

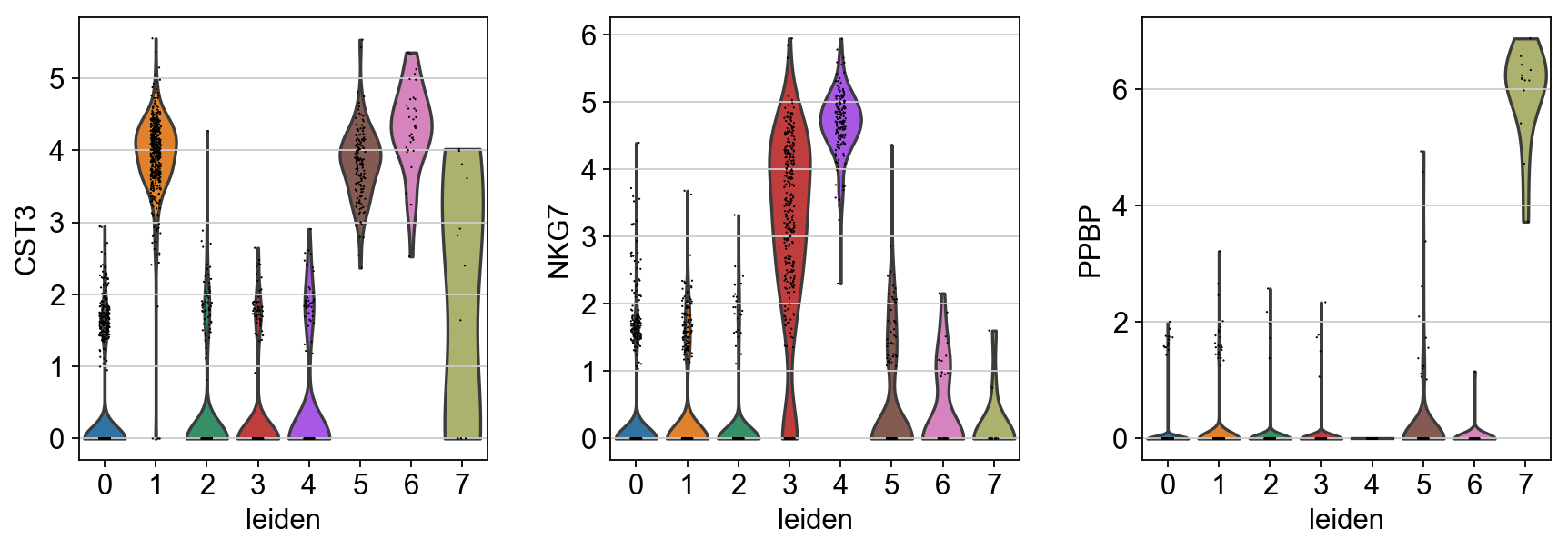
sc.pl.violin(adata, ['CST3', 'NKG7', 'PPBP'], groupby='leiden')

Actually mark the cell types.

new_cluster_names = [
    'CD4 T', 'CD14 Monocytes',
    'B', 'CD8 T',
    'NK', 'FCGR3A Monocytes',
    'Dendritic', 'Megakaryocytes']
adata.rename_categories('leiden', new_cluster_names)

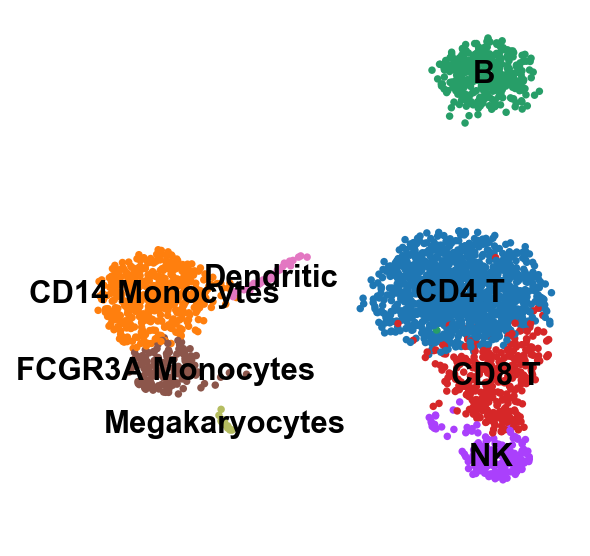
sc.pl.umap(adata, color='leiden', legend_loc='on data', title='', frameon=False, save='.pdf')

WARNING: saving figure to file figures/umap.pdf

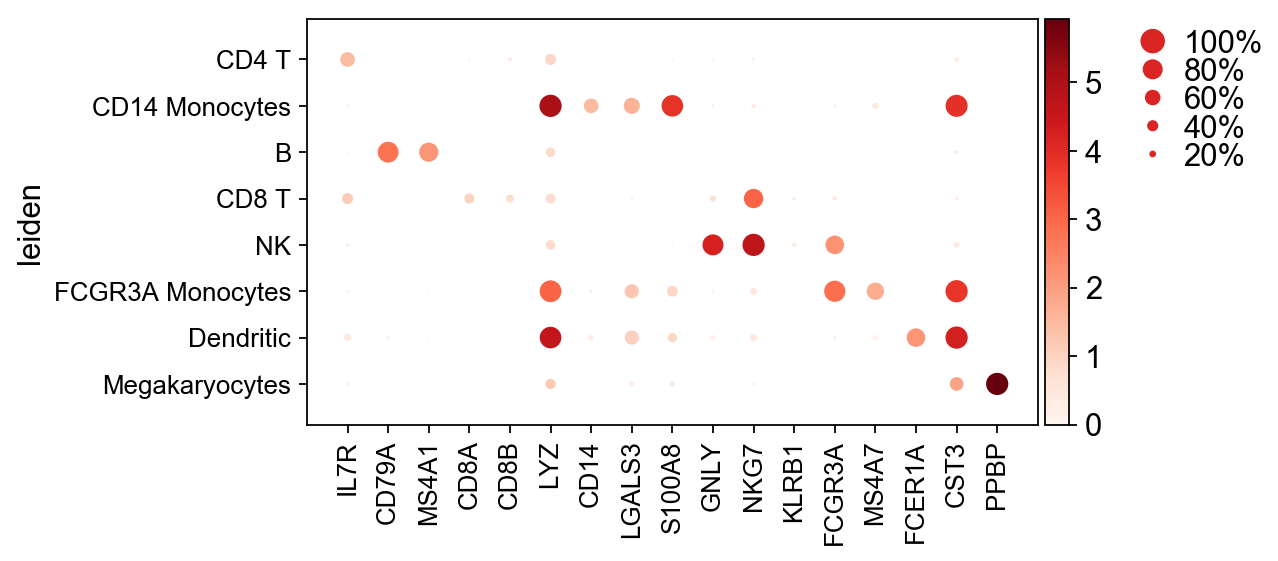
Now that we annotated the cell types, let us visualize the marker genes.

ax = sc.pl.dotplot(adata, marker_genes, groupby='leiden')

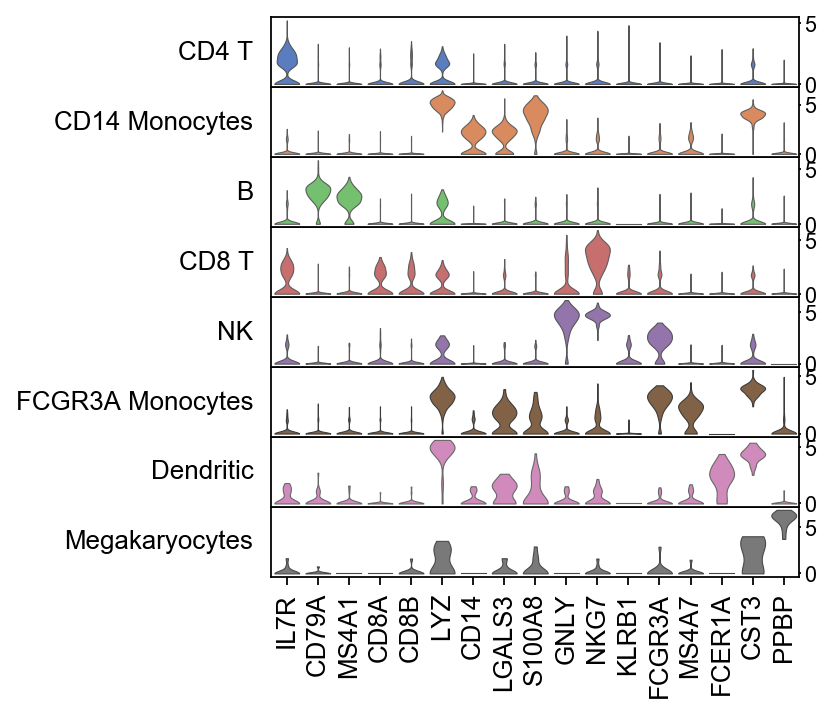
There is also a very compact violin plot.

ax = sc.pl.stacked_violin(adata, marker_genes, groupby='leiden', rotation=90)

During the course of this analysis, the AnnData accumlated the following annotations.

adata

AnnData object with n_obs × n_vars = 2638 × 1838
    obs: 'n_genes', 'percent_mito', 'n_counts', 'leiden'
    var: 'gene_ids', 'n_cells', 'highly_variable', 'means', 'dispersions', 'dispersions_norm'
    uns: 'leiden', 'leiden_colors', 'neighbors', 'pca', 'rank_genes_groups', 'umap'
    obsm: 'X_pca', 'X_umap'
    varm: 'PCs'

adata.write(results_file, compression='gzip')  # `compression='gzip'` saves disk space, but slows down writing and subsequent reading

Get a rough overview of the file using h5ls, which has many options - for more details see here. The file format might still be subject to further optimization in the future. All reading functions will remain backwards-compatible, though.

If you want to share this file with people who merely want to use it for visualization, a simple way to reduce the file size is by removing the dense scaled and corrected data matrix. The file still contains the raw data used in the visualizations.

adata.X = None
adata.write('./write/pbmc3k_withoutX.h5ad', compression='gzip')

If you want to export to “csv”, you have the following options:

# Export single fields of the annotation of observations
# adata.obs[['n_counts', 'louvain_groups']].to_csv(
#     './write/pbmc3k_corrected_louvain_groups.csv')

# Export single columns of the multidimensional annotation
# adata.obsm.to_df()[['X_pca1', 'X_pca2']].to_csv(
#     './write/pbmc3k_corrected_X_pca.csv')

# Or export everything except the data using `.write_csvs`.
# Set `skip_data=False` if you also want to export the data.
# adata.write_csvs(results_file[:-5], )